Introducción:
En Excel, una de las funciones más utilizadas es la de hallar la ecuación de una recta. Esto es especialmente útil en campos como la estadística, la ingeniería y las ciencias naturales. En esta guía paso a paso, te mostraré cómo calcular la ecuación de una recta utilizando Excel. Ya sea que estés realizando un proyecto de investigación o necesites realizar análisis de datos, este tutorial te ayudará a dominar esta habilidad clave.
¿Qué es una ecuación de una recta?
Antes de adentrarnos en los pasos para encontrar la ecuación de una recta en Excel, es importante entender qué es realmente una ecuación de una recta. En términos simples, una ecuación de una recta representa una línea recta en un plano cartesiano. Está compuesta por dos variables, x e y, y sus respectivos coeficientes. La ecuación general de una recta es:
y = mx + b
Donde m es la pendiente de la recta y b es la ordenada al origen. En Excel, podemos utilizar una herramienta llamada “Regresión Lineal” para calcular estos valores y obtener la ecuación de la recta.
Paso 1: Organizar tus datos
El primer paso para calcular la ecuación de una recta en Excel es organizar tus datos en una tabla. Debes tener al menos dos conjuntos de datos: uno para las variables x y otro para las variables y. Asegúrate de que tus datos estén en columnas separadas para facilitar el cálculo.
Paso 2: Insertar gráfico de dispersión
Una vez que tengas tus datos organizados, el siguiente paso es crear un gráfico de dispersión en Excel. Esto te permitirá visualizar tus datos y determinar si existe una relación lineal entre ellos.
Para insertar un gráfico de dispersión, selecciona tus datos y ve a la pestaña “Insertar” en la barra de herramientas de Excel. A continuación, elige el tipo de gráfico de dispersión que desees utilizar.
Una vez que hayas completado esta acción, Excel generará automáticamente el gráfico de dispersión utilizando tus datos. Ahora podrás visualizar tus puntos de datos en el gráfico.
Paso 3: Agregar línea de regresión
El siguiente paso es agregar una línea de regresión a tu gráfico de dispersión. Esta línea representará la ecuación de la recta que mejor se ajusta a tus puntos de datos.
Para agregar una línea de regresión, haz clic derecho en cualquier punto de datos en el gráfico y selecciona la opción “Agregar línea de tendencia” en el menú desplegable. Aparecerá una ventana con diferentes opciones de línea de tendencia.
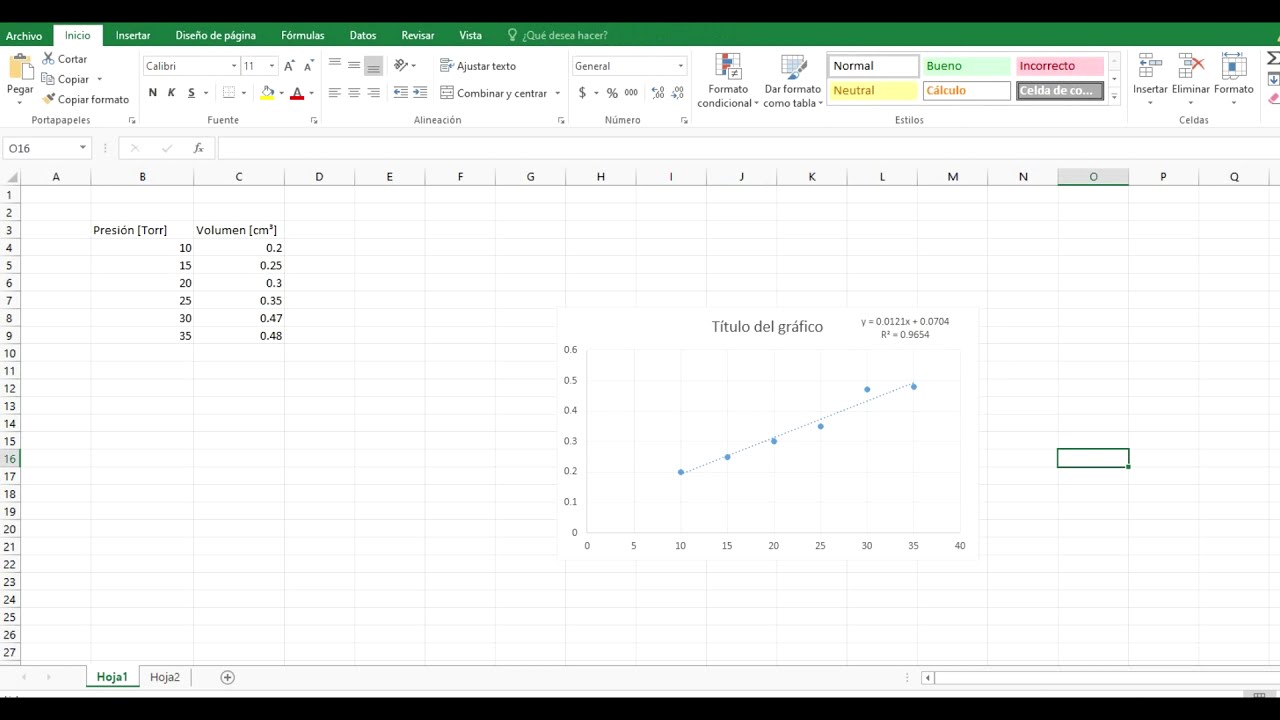
Selecciona la opción “Lineal” y marca la casilla “Mostrar ecuación en el gráfico”. Esto hará que se muestre la ecuación de la recta en el gráfico.
Paso 4: Interpretar la ecuación de la recta
Una vez que hayas agregado la línea de regresión y la ecuación de la recta a tu gráfico, podrás interpretar los valores de la pendiente (m) y la ordenada al origen (b) en la ecuación de la recta.
La pendiente (m) indica la inclinación de la recta. Si es positivo, la recta se inclinará hacia arriba de izquierda a derecha. Si es negativo, la recta se inclinará hacia abajo de izquierda a derecha.
La ordenada al origen (b) indica el punto en el que la recta cruza el eje y. Si b es positivo, la recta cortará el eje y por encima del origen. Si b es negativo, cortará por debajo del origen.
Preguntas frecuentes
1. ¿Puedo utilizar la función “Regresión Lineal” en Excel con más de dos conjuntos de datos?
Sí, puedes utilizar la función “Regresión Lineal” en Excel con más de dos conjuntos de datos. Simplemente asegúrate de organizar tus datos en columnas separadas y seguir los mismos pasos descritos anteriormente.
2. ¿La ecuación de la recta calculada en Excel es precisa?
La ecuación de la recta calculada en Excel es una aproximación basada en tus datos. Si tus datos siguen una relación lineal, la ecuación calculada será bastante precisa. Sin embargo, si tus datos presentan una dispersión significativa, la ecuación puede no ser tan precisa.
Conclusión:
Calcular la ecuación de una recta en Excel puede ser una herramienta útil para analizar datos y realizar proyectos de investigación. Sigue esta guía paso a paso y podrás dominar esta habilidad rápidamente. Recuerda que la pendiente y la ordenada al origen son clave para interpretar la ecuación de la recta y entender la relación entre tus variables. ¡Buena suerte!